Rabin signature algorithm
In cryptography the Rabin Signature Scheme is a method of Digital signature originally proposed by Michael O. Rabin in 1979. The Rabin Signature Scheme was one of the first digital signature schemes proposed, and it was the first to relate the hardness of forgery directly to the problem of integer factorization. Because of its simplicity and prominent role in early public key cryptography, the Rabin Signature Scheme is covered in most introductory courses on cryptography. The Rabin Signature Scheme is existentially unforgeable in the random oracle model assuming the integer factorization problem is intractable. The Rabin Signature Scheme is also closely related to the Rabin cryptosystem.
Contents |
Original Algorithm
The algorithm relies on a collision-resistant hash function 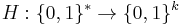
- Key Generation
- The signer S chooses primes p,q each of size approximately k/2 bits, and computes the product
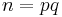
- S then chooses a random b in
 .
. - The public key is (n,b)
- The private key is (p,q)
- The signer S chooses primes p,q each of size approximately k/2 bits, and computes the product
- Signing
- To sign a message m the signer S picks random padding U and calculates H(mU)
- S then solves
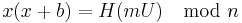
- If there is no solution S picks a new pad U and tries again. If H is truly random the expected number of tries is 4.
- The signature on m is the pair (U,x)
- Verification
- Given a message m and a signature (U,x) the verifier V calculates x(x+b) and H(mU) and verifies that they are equal
Modern Terminology
In modern presentations, the algorithm is often simplified as follows
The hash function H is assumed to be a random oracle and the algorithm works as follows
- Key Generation
- The signer S chooses primes p,q each of size approximately k/2 bits, and computes the product
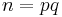
- The public key is n
- The private key is (p,q)
- The signer S chooses primes p,q each of size approximately k/2 bits, and computes the product
- Signing
- To sign a message m' the signer S picks random padding U and calculates H(mU)
- If H(mU) is not a square modulo n, S picks a new pad U
- S solves the equation
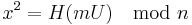
- The signature on m is the pair (U,x)
- Verification
- Given a message m and a signature (U,x) the verifier V calculates x2 and H(mU) and verifies that they are equal
In some treatments, the random pad U is eliminated and instead we add two numbers a and b to the public key with 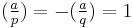 and
and 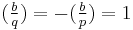 where
where 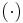 denotes the legendre symbol. Then for any r modulo n exactly one of the four numbers
denotes the legendre symbol. Then for any r modulo n exactly one of the four numbers 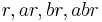 will be a square, and the signer chooses that one for his signature.
will be a square, and the signer chooses that one for his signature.
Security
If H is a random oracle, i.e. its output is truly random in 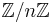 then, forging a signature on any message m is as hard as calculating the square root of a random element in
then, forging a signature on any message m is as hard as calculating the square root of a random element in 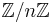 . To see that taking a random square root is as hard as factoring, we first note that any square modulo n has four square roots since n has two square roots modulo p and two square roots modulo q, and each pair gives a unique square root modulo n by the chinese remainder theorem. Now, if we have two different square roots, x,y such that
. To see that taking a random square root is as hard as factoring, we first note that any square modulo n has four square roots since n has two square roots modulo p and two square roots modulo q, and each pair gives a unique square root modulo n by the chinese remainder theorem. Now, if we have two different square roots, x,y such that 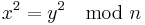 but
but 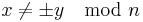 , then this immediately leads to a factorization of n since n divides
, then this immediately leads to a factorization of n since n divides 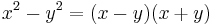 but it does not divide either factor. Thus taking
but it does not divide either factor. Thus taking 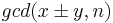 will lead to a nontrivial factorization of n. Now, there exists an algorithm to take square roots, we pick a random r modulo n and square it
will lead to a nontrivial factorization of n. Now, there exists an algorithm to take square roots, we pick a random r modulo n and square it  , then, using the algorithm to take the square root of R modulo n, we will get a new square root
, then, using the algorithm to take the square root of R modulo n, we will get a new square root 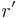 , and with probability half
, and with probability half 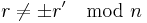 .
.